Curso: Introducción a la teoría de fibrados vectoriales y clases características (Omegar Calvo Andrade, 12-14 de enero de 2022)
Se impartirá en la universidad de Valladolid los días 12, 13 y 14 de enero en horario de 10:00-11:30, en el aula 306 de la Facultad de Ciencias.
Además, se podrá seguir de forma remota en el siguiente enlace:
Wednesday, 12 Jan, 2022 10:00 | 2 hours | (UTC+01:00) Brussels, Copenhagen, Madrid, Paris
Occurs every day effective 12/1/2022 until 14/1/2022 from 10:00 to 12:00, (UTC+01:00) Brussels, Copenhagen, Madrid, Paris
Meeting number: 2730 480 2961
Password: bBeXztqH373
Occurs every day effective 12/1/2022 until 14/1/2022 from 10:00 to 12:00, (UTC+01:00) Brussels, Copenhagen, Madrid, Paris
Meeting number: 2730 480 2961
Password: bBeXztqH373
Resumen:
I sesión:
1) Dos teoremas clásicos:
Teorema de Gauss-Bonnet.
Teorema de Poincaré-Hopf.
2) Fibrados vectoriales de rango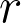 
y secciones.
y secciones. i) 
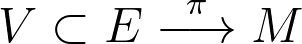donde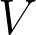 
es un espacio vectorial de =r "dim(V)=r")
sobre 
o 
.
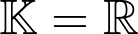donde es un espacio vectorial de sobre o 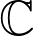. ii) %5F%7B%5Cmathcal%7BA%7D%7D "Vect^r_{\mathbb{K}}(M)_{\mathcal{A}}")
Clases de equivalencia módulo isomorfismo de rango 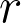de fibrados vectoriales en la categoría 
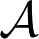cómo
Clases de equivalencia módulo isomorfismo de rango de fibrados vectoriales en la categoría cómo  "H^1(M,GL(n,\mathcal{A})")
, dónde 
o 
para el caso holomorfo. iii) Fibrados Tautológicos sobre la variedad de Grassman y fibrado universal.
![Vect^r_{\mathbb{K}}(M)_{\mathcal{C}^{\infty}}=[M,Gr_{\mathbb{K}}(M)]](https://ci5.googleusercontent.com/proxy/2IcseavwXRczHwEVyPy8hP9sIMUPla8y2_jnxePznJ5qn5kgTzKE5xaExZio7epnSOUwB2dN198cvl-pwjdA2qB0PITgbWc-6gu4Solse_jIQftkDXL10DuAYCJuByBNMwePwj-b8ktsyujJx3eK4qEyrzw3LJO2XVXAMhwwucmHZYUJekv3DksSyShI4sYoxdVSGkmXMqEaM-sqm5WGRb-_0fwjNfpHLKFromckQxt6d5Zmmu38YNHcsxdj38eLXyXPej_U0Q=s0-d-e1-ft#https://s0.wp.com/latex.php?zoom=3&bg=ffffff&fg=000000&s=0&latex=Vect%5Er%5F%7B%5Cmathbb%7BK%7D%7D(M)%5F%7B%5Cmathcal%7BC%7D%5E%7B%5Cinfty%7D%7D=[M,Gr%5F%7B%5Cmathbb%7BK%7D%7D(M)] "Vect^r_{\mathbb{K}}(M)_{\mathcal{C}^{\infty}}=[M,Gr_{\mathbb{K}}(M)]")
Ejemplo: Orientación como un elemento de
%5Cni%09E%5Cmapsto%09w%5F1(E)%5Cin%09H%5E1(M,%5Cmathbb%7BZ%7D%5F2) "Vect^r_{\mathbb{R}}(M)\ni E\mapsto w_1(E)\in H^1(M,\mathbb{Z}_2)")
iv) Definición axiomática de clases de Chern (caso complejo).
v) Idea de la construcción de las clases de Chern (Principio de escisión).
II Sesión:
1) Conexiones (concepto de derivar secciones) y curvatura.
2) Definición en términos de la curvatura (Teoría de Chern-Weil) en  "H^{\ast}_{DR}(M)")
.
. 3) Ejemplo de fibrados de Líneas: =%5Cfrac%7B1%7D%7B2%5Cpi%09i%7D%5Cint%5FM%09%5CTheta "c_1(L)=\frac{1}{2\pi i}\int_M \Theta")
cuando 
es una superficie de Riemann y 
un fibrado de líneas.
cuando es una superficie de Riemann y 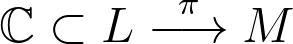un fibrado de líneas.III Sesión:
Aplicaciones:
Teorema de Índice normal de Camacho-Sad.
Aplicación a Foliaciones y distribuciones con singularidades.